The Quest for the Anti-Me - Truth in Tables
Hi, and welcome back to Deeply Curious! We’re still goofing around in Latent Space. Last time, I promised we’d “go way too deep into age, gender, and smileyness… and then keep going!” That’s still coming, but first, we must find fill a table, with truth!
What’s a Latent Direction?
As you may recall, last time I found myself in latent space. That is to say, I found the big list (the “vector”) of numbers (or “latents”), that, when fed into the program, generates my face:

The really cool thing about these “latent vectors”, is that there are… directions you can go. And often, those directions are understandable by people.
So, for example, you can take a whole bunch of latent vectors of people smiling, and another group of people frowning, and do something like:
(smiling people) - (not smiling people) = [some new big list of numbers]
That new list of numbers describes (approximately) the “smiling/not-smiling” direction. So then you take that, and add it to a latent vector that describes someone’s face, and get something like this:
 (In this picture, from the original Stylegan-Encoder repo by Puzer, Puzer has managed to find a latent direction that describes frowning/smiling. They then added and subtracted that latent direction to pictures of famous politicians. The original photos are down the center.)
(In this picture, from the original Stylegan-Encoder repo by Puzer, Puzer has managed to find a latent direction that describes frowning/smiling. They then added and subtracted that latent direction to pictures of famous politicians. The original photos are down the center.)
I was wondering whether I’d be able to do anything like this myself, given the right pairs of pictures. I went out into a local park with my friend, and we took a set of 8 pictures…
The Truth Table
So, I was wondered what the difference would be,
- between hatted me,
- and smiling me,
- and with my glasses on so I can see.
So I made the combinations of all three!
(This sort of layout, where you write down every combination in yes/no format, is called a “Truth Table”)
| Hat | Glasses | Smile | Original File | Generated after a While |
|---|---|---|---|---|
| no | no | no |  Aligned original: MG_4138 Aligned original: MG_4138 |
 4500 iterations, FID=0.12 4500 iterations, FID=0.12 |
| no | no | ya |  Aligned original: MG_4142 Aligned original: MG_4142 |
 3600 iterations, FID=0.14 3600 iterations, FID=0.14 |
| no | ya | no |  Aligned original: MG_4139 Aligned original: MG_4139 |
 9868 iterations, FID=0.09 9868 iterations, FID=0.09 |
| no | ya | ya |  Aligned original: MG_4143 Aligned original: MG_4143 |
 11400 iterations, FID=0.13 11400 iterations, FID=0.13 |
| Hat | Glasses | Smile | Original File | Generated after a While |
| ya | no | no |  Aligned original: MG_4137 Aligned original: MG_4137 |
 1500 iterations, FID=0.19 1500 iterations, FID=0.19 |
| ya | no | ya |  Aligned original: MG_4141 Aligned original: MG_4141 |
 13000 iterations, FID=0.08 13000 iterations, FID=0.08 |
| ya | ya | no |  Aligned original: MG_4136 Aligned original: MG_4136 |
 57000 iterations, FID<0.05 57000 iterations, FID<0.05 |
| ya | ya | ya |  Aligned original: MG_4140 Aligned original: MG_4140 |
 12000 iterations, FID<0.16 12000 iterations, FID<0.16 |
Bonus Image
 Me, with Cowboy Hat on. 19688 iterations, FID=0.12
Me, with Cowboy Hat on. 19688 iterations, FID=0.12
Note: this took forever to do. I had to roll balls down hills for hours.
Next time: Can we roll a ball down a hill more efficiently?
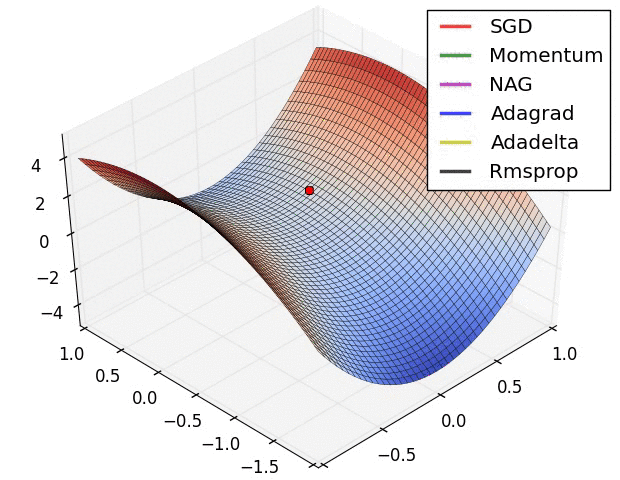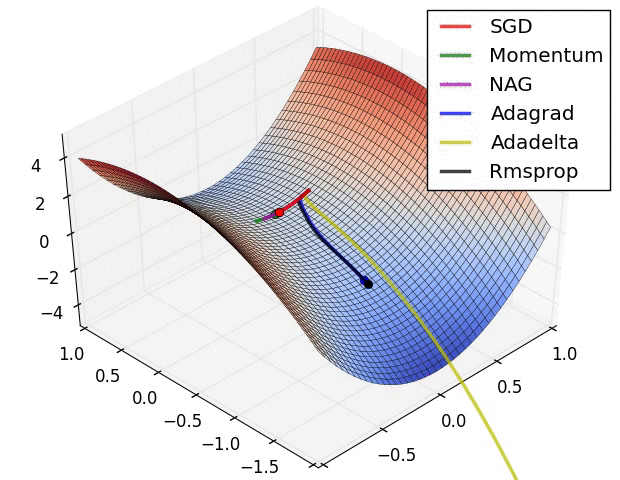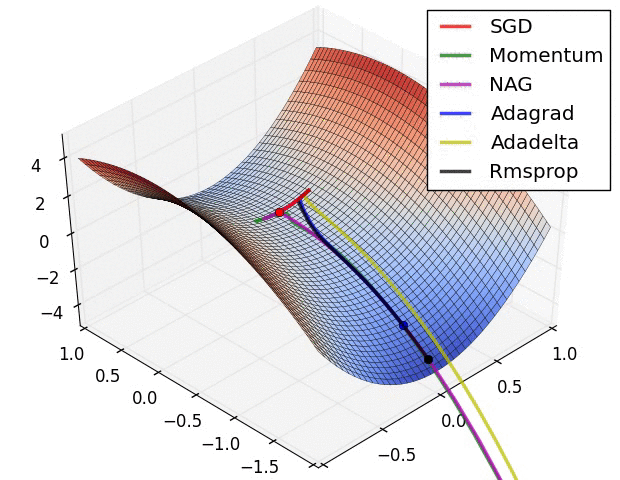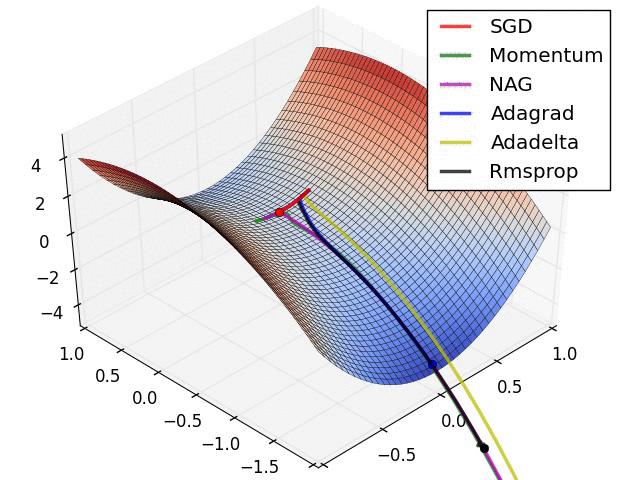
(Image from “An overview of gradient descent optimization algorithms” by Sebastian Ruder, who credits Alec Radford)